|
理论教学
|
|
 |
|

|
|
|
| 利用滴定曲线方程和Origin精确绘制滴定曲线* |
| 池泉**, 王献 |
| 中南民族大学化学与材料科学学院 湖北武汉 430074 |
|
| Plotting Titration Curves Accurately with Origin Using Titration Curve Equations |
| CHI Quan**, WANG Xian |
| College of Chemistry and Materials Science, South-Central University for Nationalities, Wuhan 430074, China |
|
|
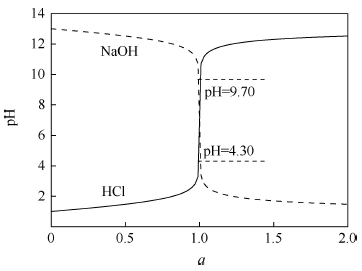
摘要:滴定曲线是滴定分析原理的重要内容。它显示了滴定过程中平衡体系性质的变化,可以获知化学计量点和滴定突跃信息,从而指导准确滴定判别或指示剂的选择。滴定曲线方程是滴定过程中体系的某种性质X(例pH)与滴定分数a(或滴定剂体积V)的关系方程,解析方程可获得函数X=f(a)的表达式。对一些较复杂的体系,推导函数X=f(a)较困难,但多数情况下反函数a=g(X)的推导更容易,表达式也更简洁。本文对酸碱、配位、氧化还原和沉淀滴定曲线方程进行了系统总结,并对不同情况下的函数X=f(a)或反函数a=g(X)进行了推导,拓展了教材内容。根据函数关系,在Origin中利用其函数绘图功能可直接绘制出滴定曲线,不用先生成数据点再绘图,方便快捷。用反函数绘图时增加数据点即可获得高精度的滴定曲线,可直接从滴定曲线上查找化学计量点和滴定突跃信息。
|
|
| 关键词: 滴定曲线,
滴定曲线方程,
Origin,
反函数
|
|
|
| 基金资助:*中南民族大学教学研究项目(JYZD18032) |
|
通讯作者:
**E-mail:chi_quan@163.com
|
| 引用本文: |
|
池泉, 王献. 利用滴定曲线方程和Origin精确绘制滴定曲线*[J]. 化学教育(中英文), 2020, 41(2): 21-27
|
|
| [1] |
李龙泉, 朱玉瑞, 金谷, 等. 定量化学分析. 2版. 合肥: 中国科学技术大学出版社, 2005
|
| [2] |
邵利民.化学通报, 2016, 79(2): 187-191
|
| [3] |
孙晓波, 王进平. 大学化学, 2015, 30(4): 78-85
|
| [4] |
王进平, 孙晓波. 大学化学, 2014, 29(6): 29-33
|
| [5] |
徐守兵. 化学教学, 2007(11): 58-60
|
| [6] |
丁荫祥. 龙岩师专学报, 2002(3): 71-72
|
| [7] |
孟凡昌, 杨代菱. 大学化学, 2001(2): 30-34
|
| [8] |
罗济文. 广西师范大学学报(综合专辑), 1995(S1): 257-259
|
| [9] |
武汉大学主编. 分析化学上册. 6 版. 北京: 高等教育出版社, 2016
|
| [10] |
邵利民. 分析化学. 北京: 科学出版社, 2016
|
|
|
|