|
化学奥林匹克
|
|
 |
|

|
|
|
| 化学平衡解题通用方法探讨* |
| 徐嘉伟, 邓力克, 陈晓峰, 方敏, 包建春, 吴勇** |
| 南京师范大学化学与材料科学学院 江苏南京 210023 |
|
| A General Method for Solving Problems Related to Chemical Equilibrium |
| XU Jia-Wei, DENG Li-Ke, CHEN Xiao-Feng, FANG Min, BAO Jian-Chun, WU Yong** |
| School of Chemistry and Materials Science, Nanjing Normal University, Nanjing 210023, China |
|
|
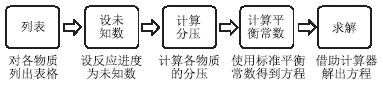
摘要:对于复杂的化学平衡,平衡时刻浓度、分压、物质的量、转化率之间存在错综复杂的关系,给解题带来了很大难度。提出了“列表—设未知数—计算分压—计算平衡常数—求解”的5步解题通用方法,并利用该方法,结合CASIO计算器独特的解题特色,对近几年化学竞赛中出现的2道化学平衡试题进行了剖析。
|
|
| 关键词: 化学竞赛,
化学平衡,
试题解析
|
|
|
| 基金资助:*南京师范大学重点教材(1812200009171705)和在线开放课程(1812200001ZXKC1705);江苏省省级大学生创新创业训练计划(N201910319079Y) |
|
通讯作者:
**E-mail: wuyong@njnu.edu.cn
|
| 引用本文: |
|
徐嘉伟, 邓力克, 陈晓峰, 方敏, 包建春, 吴勇. 化学平衡解题通用方法探讨*[J]. 化学教育(中英文), 2020, 41(23): 100-103
|
|
| [1] |
Wilbur Bergquist, Henry Heikkinen. Journal of Chemical Education, 1990, 67(12):1000-1003
|
| [2] |
姜显光, 郑长龙. 化学教育(中英文), 2019, 40(3):58-63
|
| [3] |
张霄, 董素静. 化学教育, 2016, 37(11):28-31
|
| [4] |
高盘良. 大学化学, 2012, 27(2):69-71
|
| [5] |
杨桦. 化学教育(中英文), 2017, 38 (22):34-37
|
| [6] |
韩国江. 大学化学, 2017, 32(11):81-85
|
| [7] |
余子迪. 大学化学, 2019, 34(2):90-98
|
| [8] |
常泰维, 陈胤霖, 崔竞蒙, 等. 大学化学, 2017, 32(1):106-112
|
| [9] |
傅献彩, 沈文霞, 姚天扬, 等. 物理化学(上册). 5版. 北京:高等教育出版社, 2005:352-353
|
| [10] |
吴勇, 缪震元. 普通化学. 2版. 南京:南京大学出版社, 2017:9-10
|
| [11] |
第32届中国化学奥林匹克(初赛)试题、 解答与评分标准. 北京:中国化学会, 2018
|
| [12] |
吴勇, 马宏佳. 化学教育, 2004,25(1):57-61
|
| [13] |
华中师范大学, 东北师范大学, 陕西师范大学, 等. 分析化学(上). 4版. 北京:高等教育出版社, 2011:105-107
|
|
|
|